Logistic Regression

 In this blog I will be writing about Logistic Regression, that is, what is Logistic regression, Cost function, Threshold, checking goodness of fit etc.

What  is Logistic Regression?

The logistic regression statistic modeling technique is used when we have a binary outcome variable. For example: given the parameters, will the student pass or fail? Will it rain or not? etc.

So, though we may have continuous or categorical independent variables, we can use the logistic regression modeling technique to predict the outcome when the outcome variable is binary.



Let's see how the algorithm differs from linear regression. Linear regression statistical model is used to predict continuous outcome variables, Whereas logistic regression predicts categorical outcome variables. Linear regression model regression  line is highly susceptible to outliers. So, it will not be appropriate for logistic regression.

Where to use logistic regression

Logistic regression is used to solve classification problems, and the most common use case is binary logistic regression, where the outcome is binary (yes or no). In the real world, you can see logistic regression applied across multiple areas and fields.

  • In health care, logistic regression can be used to predict if a tumor is likely to be benign or malignant.
  • In the financial industry, logistic regression can be used to predict if a transaction is fraudulent or not.
  • In marketing, logistic regression can be used to predict if a targeted audience will respond or not.

Are there other use cases for logistic regression aside from binary logistic regression? Yes. There are two other types of logistic regression that depend on the number of predicted outcomes.

The three types of logistic regression

  1. Binary logistic regression - When we have two possible outcomes, like our original example of whether a person is likely to be infected with COVID-19 or not.
  2. Multinomial logistic regression - When we have multiple outcomes, say if we build out our original example to predict whether someone may have the flu, an allergy, a cold, or COVID-19.
  3. Ordinal logistic regression - When the outcome is ordered, like if we build out our original example to also help determine the severity of a COVID-19 infection, sorting it into mild, moderate, and severe cases.

Mathematics behind Best fitted line in logistic regression

Probability always ranges between 0 (does not happen) and 1 (happens). Using our Covid-19 example, in the case of binary classification, the probability of testing positive and not testing positive will sum up to 1. We use logistic function or sigmoid function to calculate probability in logistic regression. The logistic function is a simple S-shaped curve used to convert data into a value between 0 and 1.

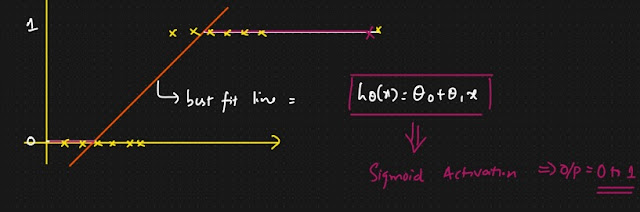
Best fitted line for logistic regression is :





Here we use same line formula were we used in linear regression, with in we apply sigmoid function. To get the output with in 0 to 1, Here there is an another topic called as threshold were we can classify the two outcome. Threshold can be selected through AUC and ROC by business problem.


Cost function in Logistic Regression:

In the case of Linear Regression, the Cost function is – MSE
                                

Here which lead to obtain the global minima by gradient decent algorithm, Which having convex function.

But for Logistic Regression, if we use MSE it leads to having local minima.


Here which lead to obtain the local minima by gradient decent algorithm, Which having non convex function.


So to obtain the global minima there is another cost function:

Log Loss  or Logit cost function:




Here which lead to obtain the global minima by gradient decent algorithm, Which having convex function.

                                   

To Minimize  the cost function:


Conclusion

In this blog, I have presented you with the basic concept of Logistic Regression. I hope this blog was helpful and would have motivated you enough to get interested in the topic.




Comments

Post a Comment

Popular posts from this blog

Ridge, Lasso And ElasticNet Regression .

Image
  OVERVIEW This blog is going to be very interested for the understanding point of view for ridge ,lasso and elastic net regression . Let first understand what is lasso and Ridge and  ElasticNet. Before moving to Ridge, Lasso and Elastic Net Regression we need an basic idea of Overfitting and Underfitting. Let have an brief idea about it. Overfitting and Underfitting    Overfitting  is a condition where bias is low but variance tends to get high and results in fitting too much in a model, whereas in  Underfitting , the variance is low but bias tends to get high and the model becomes too loose or simplified. Also, when we can’t examine anything from the  machine learning algorithm ,  we can say it is an underfitting condition, whereas, when data provides excessive information that we don’t even need and this data is acting as a burden, we say it is an overfitting problem. Graphical representation of Underfitting, Just Fitting, and Overfitting The p...
Read more

Performance Metrices for classification and Regression.

Image
  Performance Metrics in Machine Learning Evaluating the performance of a Machine learning model is one of the important steps while building an effective ML model.  To evaluate the performance or quality of the model, different metrics are used, and these metrics are known as performance metrics or evaluation metrics.  These performance metrics help us understand how well our model has performed for the given data. In this way, we can improve the model's performance by tuning the hyper-parameters. Each ML model aims to generalize well on unseen/new data, and performance metrics help determine how well the model generalizes on the new dataset. In machine learning, each task or problem is divided into  classification  and  Regression . Not all metrics can be used for all types of problems; hence, it is important to know and understand which metrics should be used. Different evaluation metrics are used for both Regression and Classification tasks. In this top...
Read more

CNN(Convolutional Neural Networks)

Image
  Introduction: Convolutional Neural Networks (CNNs) are a type of deep learning algorithm that have revolutionized the field of computer vision. They are specifically designed to process image data and have been widely adopted in applications such as image classification, object detection, and image segmentation. In this blog, we will delve into the workings of a CNN and understand its key components. The Key Components of a CNN A CNN is made up of multiple layers including convolutional layers, activation layers, pooling layers, and fully connected layers. Let's take a closer look at each of these components: Convolutional Layer: The convolutional layer is the heart of a CNN and is responsible for performing the convolution operation on the input image. The convolution operation involves applying a set of filters to the input image to extract important features. These filters can be thought of as small matrices that are multiplied with small regions of the image to produce a new ...
Read more