Ridge, Lasso And ElasticNet Regression .

 OVERVIEW

This blog is going to be very interested for the understanding point of view for ridge ,lasso and elastic net regression . Let first understand what is lasso and Ridge and ElasticNet.


Before moving to Ridge, Lasso and Elastic Net Regression we need an basic idea of Overfitting and Underfitting. Let have an brief idea about it.

Overfitting and Underfitting 

 

  • Overfitting is a condition where bias is low but variance tends to get high and results in fitting too much in a model, whereas in 
  • Underfitting, the variance is low but bias tends to get high and the model becomes too loose or simplified.


Also, when we can’t examine anything from the machine learning algorithm, we can say it is an underfitting condition, whereas, when data provides excessive information that we don’t even need and this data is acting as a burden, we say it is an overfitting problem.
Graphical representation of Underfitting, Just Fitting, and Overfitting

The picture shows the variation of data points in underfitting and over fitting under linear regression.


So, how to prevent these problems in regression? The solution is Regularization technique.

Regularization.

Regularization is a regression technique, which limits, regulates or shrinks the estimated coefficient towards zero. In other words, this technique does not encourage learning of more complex or flexible models, so as to avoid the risk of overfitting.

  • Regularization is one of the ways to improve our model to work on unseen data by ignoring the less important features.
  • Regularization minimizes the validation loss and tries to improve the accuracy of the model.
  • It avoids overfitting by adding a penalty to the model with high variance, thereby shrinking the beta coefficients to zero



What is Ridge Regression(L2 regularization)?

 
      Ridge regression is a method to perform linear regression. It is used for Reducing the overfitting condition.
     
It is used highly for the treatment of multicollinearity in regression, it means when an          independent variable is correlated in such a way that both resemble each other, 

It causes high variance among the independent variables, we can change the value of the independent variable but it will cause a loss of information.

So in Ridge regression, we make bias and variance proportional to each other, or it basically decreases the difference between actual and predictive values. 


For ridge regression:
  


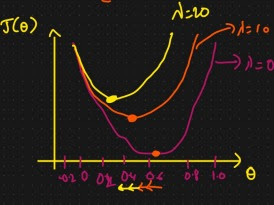
The Relation between the λ and slope is  Inversely proportional 

Note: In Ridge Regression slope(θ) value will reduce but it will never be reach zero.

What is Lasso Regression(L1 Reguralization)?


Lasso stands for Least Absolute Shrinkage Selector Operator, which is used for Reduce the features or feature selection.

  • It works the same as ridge regression when it comes to assigning the penalty for coefficient, 

  • It removes the coefficient and the variables with the help of this process and limits the bias through the below formula




The Relation between the λ and slope is  Inversely proportional 



Since if "θ" reach xero then feature will be deleted. were least correlated feature get eliminated. It is robust for outliers.

What is Elastic Net Regression?


Elastic Net is regularized linear regression technique that combine L1 & L2 Regularisation.

ENR = Lasso Regression + Ridge Regression

The equation for ENR is given below-:


Difference between Ridge, Lasso and Elastic Net Regression

 

  1. In terms of handling bias, Elastic Net is considered better than Ridge and Lasso regression, Small bias leads to the disturbance of prediction as it is dependent on a variable. Therefore Elastic Net is better in handling collinearity than the combined ridge and lasso regression.

 

  1. Also, When it comes to complexity, again, Elastic Net performs better than ridge and lasso regression as both ridge and lasso, the number of variables is not significantly reduced. Here, incapability of reducing variables causes declination in model accuracy.

 

  1. Ridge and Elastic Net could be considered better than the Lasso Regression as Lasso regression predictors do not perform as accurately as Ridge and Elastic Net. Lasso Regression tends to pick non-zero as predictors and sometimes it affects accuracy when relevant predictors are considered as non zero. 

 

Conclusion

 

Undoubtedly, regression is a widely used technique, we just read about the Ridge, Lasso, and Elastic net Regression and how they help in regularization.





 


Comments

Post a Comment

Popular posts from this blog

Performance Metrices for classification and Regression.

Image
  Performance Metrics in Machine Learning Evaluating the performance of a Machine learning model is one of the important steps while building an effective ML model.  To evaluate the performance or quality of the model, different metrics are used, and these metrics are known as performance metrics or evaluation metrics.  These performance metrics help us understand how well our model has performed for the given data. In this way, we can improve the model's performance by tuning the hyper-parameters. Each ML model aims to generalize well on unseen/new data, and performance metrics help determine how well the model generalizes on the new dataset. In machine learning, each task or problem is divided into  classification  and  Regression . Not all metrics can be used for all types of problems; hence, it is important to know and understand which metrics should be used. Different evaluation metrics are used for both Regression and Classification tasks. In this top...
Read more

CNN(Convolutional Neural Networks)

Image
  Introduction: Convolutional Neural Networks (CNNs) are a type of deep learning algorithm that have revolutionized the field of computer vision. They are specifically designed to process image data and have been widely adopted in applications such as image classification, object detection, and image segmentation. In this blog, we will delve into the workings of a CNN and understand its key components. The Key Components of a CNN A CNN is made up of multiple layers including convolutional layers, activation layers, pooling layers, and fully connected layers. Let's take a closer look at each of these components: Convolutional Layer: The convolutional layer is the heart of a CNN and is responsible for performing the convolution operation on the input image. The convolution operation involves applying a set of filters to the input image to extract important features. These filters can be thought of as small matrices that are multiplied with small regions of the image to produce a new ...
Read more